to circuits, measurements and control
H Sriyananda
Preface
This collection is the result of a very personal experience.
I was teaching courses in Circuit Theory, Electrical Measurements and in Control Systems at the University of Moratuwa for about a decade, during the period 1973 to 1982. In that year, I joined the newly established Open University, where I continued to teach for more than twenty years.
As the Open University was (and still is) severely understaffed, what I taught there varied a great deal, for I had to take on almost any course that did not happen to have a readily available teacher. This may not have contributed greatly to the quality of the learning experience for its students, but for me, it was certainly a worthwhile experience. The curriculum itself changed a number of times during this period, and during the last two years, I was teaching Principles of Electricity (at the Foundation level) and Network Theory, Digital Signal Processing and Control Systems (at the final undergraduate year).
As you would expect, the method of teaching in the two institutions differed greatly, at least superficially. Moratuwa University of the 1970s was a very much lecture-oriented university. You deliver a course of lectures, and you set an examination at the end of the year, to ascertain how much of your lecture material has been absorbed by the students. What was attempted at the Open University was a replacement of this same strategy, with pre-prepared self-study material replacing the lectures. However, a number of innovations were introduced at the Open University from its very inception.
Over the last five years, I have been forced to re-think the validity of the practices associated with formal teaching and assessment in Sri Lankan Universities, due to a number of circumstances. However, the business of education is a very conservative one, and it takes a great deal of effort to make even a small change.
When I came back to the University of Moratuwa in 2003 (on Sabbatical leave from the Open university) I found that the University of Moratuwa was in the process of introducing some of the changes that we had implemented at the Open University. As I had to get back to class-room-based teaching, it was natural for me to attempt to prepare a set of notes to help the students and me with the task of learning / teaching.
These notes were prepared for use with four different courses (Advanced Circuit Theory and Electrical measurement Systems at Level 3, Advanced Control at Level 4 and Digital Control at First year Graduate level). However, I have been struck by the remarkable continuity and interdependence of all these courses and decided to collate them together in one volume. Some material to cover the level-three course on Control Systems has also been added. From the point of view of the Open University curriculum, it covers most of the requirements for the courses on Control Systems (level 4), Network Theory (Level 5), Digital Signal Processing (Level 6) and Modern Control Systems (Level 6).
Chapter 1 - Transform methods
Chapter 2 - State and state space
Chapter 3 - Synthesis of analogue circuits
The following table [under construction] is a rough guide on how this material may be used for the different courses.
| Course | Course content (Chapters / Sections) |
|
|---|---|---|
| University of Moratuwa | Advanced Circuit Theory | 1.1, 2.1, 2.2, 2.3, 3.1, 3.2, 3.3 |
| Electrical Measurement Systems | ||
| Advanced Control | ||
| Digital Control | ||
| The Open University | Control Systems | |
| Network Theory | ||
| Digital Signal Processing | ||
| Modern Control Systems | ||
In the classroom, these lectures were presented with a lot of reference material (mostly from the Internet), some assignments and projects. The students were expected to present their project work for the whole group for discussion and suggestions. Some of the students work (from both the Open university and the University of Moratuwa) is included in the Appendix. As these are based on notes prepared by me over a period of time extending over twenty years, I have invariably drawn on a large number of sources, including published material. However, the choice and order in which they are presented, as well as their final form is my own. I regret very much my inability to acknowledge individually the numerous sources from which I have drawn.
Introduction
We are going to attempt a look at some of the core material covered in a typical undergraduate course in Engineering, but in a somewhat different perspective. I believe that we would stand to gain a better insight into the material usually covered in courses on Circuit and Network Theory, Measurement Systems, Signal Processing and Control Systems if we look at them together, for there is a lot of common ground between them, and an understanding of one would help in the other.
I have called this approach a “systems” approach, for the defining characteristic of a system is the presence of interconnections, The one thing common to all these is that they deal with interconnected entities where the nature and form of the interconnection, the structure, is all important.
For example, in circuit theory, we will look at the behaviour of interconnected circuit elements, how they respond to excitations of various types. The behaviour of individual idealised circuit elements is used to construct the behaviour of their combinations. The structure of the interconnection, its topology, determines how the individual elements interact and thus determine the response of the whole. Similarly, in measurement systems, we look at the total behaviour of an integrated system consisting not only of an isolated sensor, but the complete system which may include complex data processing and transmission links, conversions (say from analogue to digital or digital to analogue form) etc.
In our studies we need to learn to both analyse and synthesise – to subdivide and to put together. This is because our abilities of concentration and attention are limited. Even though we are interested in the behaviour of a complete system, we are sometimes unable to comprehend its characteristics due to shear complexity. Then we divide the system into smaller subsystems, study them separately, then put them together and try to figure out how the various subsystems affect each other. This of course is not an ideal situation, but we seem to have no alternative.
What constitutes a system and what constitutes a subsystem depends on our perspective. In the example of a measurement system in the previous paragraph, I refered to the sensor as a single element. It is so when looked at from the point of view of the complete measurement system, but on the other hand, the sensor itself will contain a large number of interacting components and can be legitimately viewed as a system in its own right.
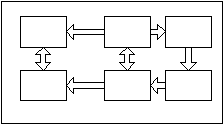
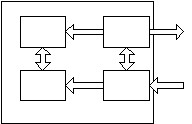This brings us the concept of closed and open systems.
A closed system is one that is totally self-contained [figure on left] – there are no connections to the outside world through which information (or energy) can flow. I cannot think of any such closed system in real life.
Other systems are open systems [figure on right] – with links to the outside world. Open systems have connections to the outside world through the system boundary, and information (or energy or even matter) may flow through these links. It is this idea that allows us to define the system boundaries as we please, and consider a subsystem as a system on its own right when necessary.
There are other concepts necessary before we start on our investigation of systems. A system may be either static or dynamic. A static system does not change with time, while a dynamic system does. Again, in real life, I have not come across any static systems, for all things are subject to change. But in our limited studies, we define the time frame of interest, and the type of change of interest, and so we do talk of static systems. An example of a static system in this sense would be a purely resistive network, excited by a dc source. The moment we include capacitive or inductive elements, we will need to consider the transient behaviour of the circuit even when the excitation is dc.
Almost all of our discussion will relate to dynamic systems, that is, systems whose response is a function of time.
In everyday life we are used to the concept of continuous time so that we naturally think in terms of any variable as a function of time. However, time need not always be the most convenient independent variable. Electrical engineers, in dealing with elementary ac networks, have become used to the idea of treating frequency (instead of time) as the most natural independent variable. This has allowed us to deal with regularly varying currents and voltages in algebraic terms rather than using differential calculus, thus effecting an enormous simplification.
Another way of treating change that has gained in importance with the advent of digital systems (and the digital computer) is to look at discrete time, rather than continuous time.
With all these possibilities of different ways of looking at phenomena, we need to be able to transform from one system of independent variable to another.